文章目录
今天是1024程序员节,祝各位节日快乐啦!!!
前导 我们之前使用位图 bitset,只能将一个整数映射到比特位上,来判断某个数是否存在
但是假如我们也想把判断一个字符串是否存在呢?布隆过滤器
布隆过滤器 特点
对于不存在的值,查找一定是不存在
对于存在的值,查找可能会不准确
映射方式 我们之前学过 hash,字符串映射可以有字符串映射的hash函数,把对应的字符串映射到某个位置上,但是如果我们也使用那样的方式会出现什么问题呢?
对于不存在的字符串,我们使用hash检测,没有问题
但是对于存在的自负床,那么就有可能会出现hash冲突的,可能会出现误判,
这里我们无法解决冲突的问题,那么我们就要尽可能的降低冲突
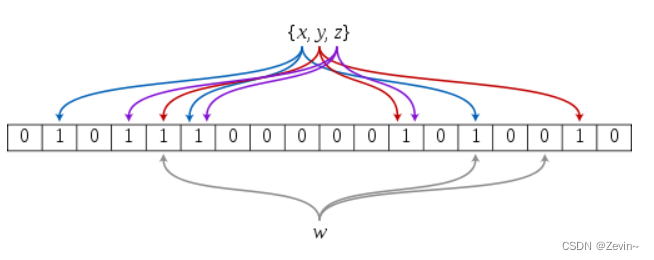
所以我们就要对一个字符串使用多个hash函数映射 ,映射到不同的地方,来降低冲突
hash 函数 这里我们运用3个hash函数,来索引到不同的位置
BKDRHash
1 2 3 4 5 6 7 8 9 10 11 12 13 struct BKDRHash size_t operator () (const string &key) {size_t ret = 0 ;for (auto e : key)31 ;return ret;
APHashs
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 struct APHash size_t operator () (const string &s) {size_t hash = 0 ;size_t ch;for (long i = 0 ; i < s.size (); i++)if ((i & 1 ) == 0 )7 )) ^ s[i] ^ (hash >> 3 );else 11 )) ^ s[i] ^ (hash >> 5 );return hash;
DJBHash
1 2 3 4 5 6 7 8 9 10 11 12 struct DJBHash size_t operator () (const string &s) {size_t hash = 5381 ;for (auto ch : s)5 ) + ch;return hash;
BloomFilter 1 2 3 4 5 6 7 8 template <size_t N, class K = string, class HashFunc1 = BKDRHash, class HashFunc2 = APHash, class HashFunc3 = DJBHash> class BloomFilterprivate :4 > _bs; public :void set (const K &key) bool test (const K &key)
set 把一个字符串设置进bloomfilter里面
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 void set (const K &key) size_t len = 4 * N;size_t index1 = h1 (key) % len;size_t index2 = h2 (key) % len;size_t index3 = h3 (key) % len;set (index1);set (index2);set (index3);
test
因为我们映射到了3个不同的位置,所以如果一个索引位不在,就不在,但是如果3个索引位都在,它大概率就在,但也会出现误判
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 bool test (const K &key) size_t len = 4 * N;size_t index1 = h1 (key) % len;size_t index2 = h2 (key) % len;size_t index3 = h3 (key) % len;if (_bs.test (index1) == false )return false ;if (_bs.test (index2) == false )return false ;if (_bs.test (index3) == false )return false ;return true ;
reset 我们需要删除吗?
其实对于bloom过滤器来说,我们不需要删除
原因
把对应的位删除,删除自己的同时可能会把和别人冲突的位也删掉了,会影响到别的值
那么如何扩展一下,使得布隆过滤器能够支持删除
每个位置存储多个bit位,存储引用计数,(有多少个值映射到了当前的位置)缺点
使用引用计数可以支持删除,但是整体消耗空间变多了,达不到我们的目的,所以我们还是尽量不支持删除
相关问题
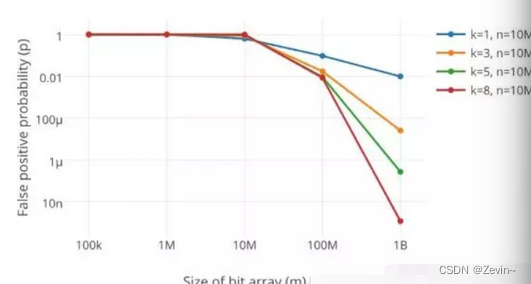
一个数映射到多个位置,我们给的布隆过滤器长度偏小,很容易映射满,出错率高,所以布隆过滤器长度大,出错率低
哈希函数越多,映射位置越多,准确性高,但是效率低,所以哈希函数个数和效率成反比,和准确率成正比
应用 使用场景
数据量大 ,节省空间 ,允许误判 ,这样的场景,就可以使用布隆过滤器
用户注册
用户进行注册页面时候输入昵称 ,密码
垃圾邮件
如果是垃圾邮件,就可以把它放到一个垃圾邮箱里面,就标记一个黑名单,放到布隆过滤器里面,
总结:利用布隆过滤器可以减少和磁盘的IO,或者网络请求,因为访问本地的数据库速度很慢,更不要说跨网络数据传递
示例 给两个文件,分别由100亿个query,我们只有1G内存,如何找到两个文件的交集?分别用精确和近似的算法
近似 :把这分别的两份100亿的query查询都放进布隆过滤器,两个地方都存在就是交集,都不存在就不是交集,这个时候是近似的交集(但是会存在不是交集的进去)
但是如果想要使用准确的算法,我们就需要使用哈希切分
哈希切分 1 2 3 4 5 6 7 8 9 10 11 12 13 14 哈希切分就可以实现精确查询100 G,那么切成多份,但是我们需要使用哈希切,而不是平均切query ,使用hash算法,如i=BKDRhash(query )query 就进入ai好的小文件query 一定进入了编号相同的小文件
例子 1 2 3 4 5 6 7 8 9 <u>一个超过100 G的log file log 中存这IP地址,涉及算法找到出现次数最多的IP(统计次数),如何找到TOPK的IP,如何直接使用Linux系统命令</u>200 ;map 统计一个小文件中的ip的次数,就是它准确的次数pair <string ,int> maxCountIP10 个ippair <string ,int>,vector<pair <string ,int>>,greater> minhead;小堆
 * 公式
* 公式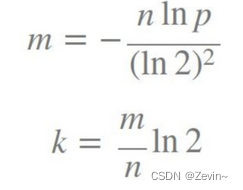 k 为哈希函数个数,m 为布隆过滤器长度,n 为插入的元素个数,p 为误报率
k 为哈希函数个数,m 为布隆过滤器长度,n 为插入的元素个数,p 为误报率