二叉树的公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
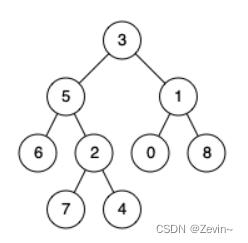
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
保存路径法
记录从根到对应节点的路径,找到最近公共节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| class Solution {
public:
bool findpath(stack<TreeNode*>& con,TreeNode* root,TreeNode* x)
{
if(root==nullptr)
return false;
con.push(root);
if(root==x)
return true;
if(findpath(con,root->left,x))
{
return true;
}
if(findpath(con,root->right,x))
return true;
con.pop();
return false;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
stack<TreeNode*> pstack;
stack<TreeNode*> qstack;
findpath(pstack,root,p);
findpath(qstack,root,q);
int diff=pstack.size()-qstack.size();
if(diff<0)
diff=-diff;
bool plarger=pstack.size()>qstack.size();
bool qlarger=!plarger;
while(diff--)
{
if(plarger)
pstack.pop();
else if(qlarger)
qstack.pop();
}
while(!pstack.empty())
{
if(pstack.top()==qstack.top())
return pstack.top();
else
{
pstack.pop();
qstack.pop();
}
}
return nullptr;
}
};
|
查找节点法
如果要找的节点在左右两边,那么我就是节点,如果都在左边,就去左边找,如果都在右边,就去右边找
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| class Solution {
public:
bool find(TreeNode* root,TreeNode* x)
{
if(root==nullptr)
return false;
if(root==x)
return true;
return find(root->left,x)||find(root->right,x);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root==nullptr)
return nullptr;
if(root==p||root==q)
return root;
bool pinleft=find(root->left,p);
bool pinright=!pinleft;
bool qinleft=find(root->left,q);
bool qinright=!qinleft;
if((pinleft&&qinright)||(pinright&&qinleft))
return root;
else if(pinleft&&qinleft)
return lowestCommonAncestor(root->left,p,q);
else if(pinright&&qinright)
return lowestCommonAncestor(root->right,p,q);
return nullptr;
}
};
|
