二叉搜索树

文章目录

二叉搜索树

概念

左子树的值小于根，右子树的值大于根
根的值大于左子树，小于右子树
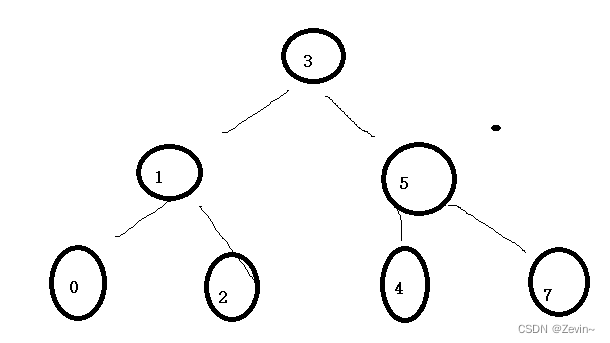
在这里插入图片描述
二叉搜索树就是用来查找的

假如我们要查找7：7比3大，到3的右子树=5，7比5大，到5的右子树7，查找到了

二叉搜索树的中序遍历，可以实现从小到大排序的遍历

时间复杂度

最坏情况1：查找：高度次
最坏情况2：O（N）:
如下图:这个效率就特别差，和单链表没有区别
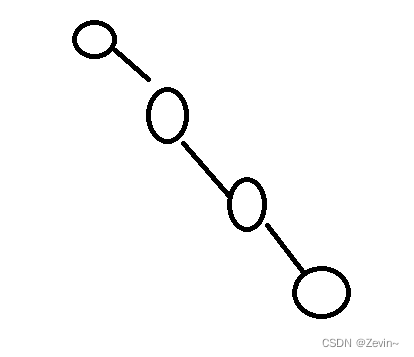
在这里插入图片描述
后续用AVL树，RB树

应用

搜索树的应用

  1. 搜索，key搜索模型，key/value模型
  2. 排序+去重

key模型
可以用来判断值在不在，效率很搞O(logN)
应用场景

  1. 搜索树存储小区业主的车牌号，扫描，存在就通过，不存在就不让过
  2. 搜索树存储同学的学号
  3. 给一个英文作文，检查里面的单词拼写是否正确（我们把单词都存放进去，进行搜索存在与否）

key/value模型
通过一个值查找另外一个值
应用场景

  1. 高铁站刷身份证进站，用身份证查早是否右买票

实现

key模型

树的节点

1
2
3
4
5
6
7
8
9
10
11
12
template <class K>

    struct BSTNode
    {
        K _val;//节点的值
        BSTNode<K> *_left;//左子树
        BSTNode<K> *_right;//右子树
        BSTNode(const K &val)//构造函数
            : _val(val), _right(nullptr), _left(nullptr)
        {
        }
    };

BStree的类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
template <class K>
    struct BSTree
    {
        typedef BSTNode<K> Node;//把每个节点进行重命名

    private:
        Node *_root;//节点

    public:
        BSTree()
            : _root(nullptr)
        {
        }
};

Insert

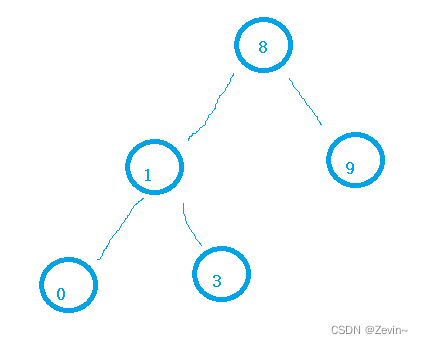
在这里插入图片描述

非递归版本

  1. 插入一个值，从根往下面走，要插入的值比它大，走右边，比它小走左边，如果这个值已近存在了，就不要插入
  2. 直到走到空，就是我们要插入的地方
  3. 我们需要把这个节点链接上去，所以我们需要空节点对应的父节点，父节点连接上新添加的节点
  4. 如果根节点就是空，直接插入在根节点即可
    例如：我们插入一个10

10>8,先走右边，到9，10>9走右边，走到了空，把它插入到这个地方

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
bool Insert(const K &key) //非线性叫做insert
{
    //插入重复的值，就返回失败
    if (_root == nullptr)//一个节点都没有
    {
        _root = new Node(key);
        return true;
    }
    else
    {
        Node *cur = _root;//cur用来走到要插入的位置
        Node *prev;//prev用来记录插入位置的父节点
        while (cur)
        {
            if (cur->_val > key)//比要插入的值大，往左走
            {
                prev = cur;
                cur = cur->_left;
            }
            else if (cur->_val < key)//比要插入的值小，往右走
            {
                prev = cur;
                cur = cur->_right;
            }
            else//相等就别走了
            {
                return false;
            }
        }
        //走到这里cur就是空
        cur = new Node(key);
        if (prev->_val < key)//父节点小于插入节点
        {
            prev->_right = cur;//连接到父节点的右边
        }
        else
        {
            prev->_left = cur;
        }
        return true;
    }
}

递归版本

我们使用引用就不需要用父节点来连接
例如:我们链接上的节点为10，走到9的右，root即是空，也是9右指针的别名

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
bool _InsertR(Node *&root, const K &key) //这里要多一个引用,指针的引用，进行修改才使用引用
{
    if (root == nullptr) //走到空就插入,引用，root是上面的root->right别名
    {
        root = new Node(key); //直接链接上了 ，都是前面的别名，都连接起来了
        return true;
    }
    if (root->_val > key)
    {
        return _InsertR(root->_left, key);
    }
    else if (root->_val < key)  
    {
        return _InsertR(root->_right, key);
    }
    else
    {
        return false;
    }
}

bool InsertR(const K &key) //有序的方式就会变成单边树，栈爆了
{
    //递归有根，都要套一个子函数
    return _InsertR(_root, key);
}

Find

非递归版本

从根节
点往下走，比它大，走右边，比它小走左边，相等就找到了，走到空就说明没找到

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
bool Find(const K &key) //查找
{
    Node *cur = _root;
    while (cur)
    {
        if (cur->_val > key)
        {
            cur = cur->_left;
        }
        else if (cur->_val < key)
        {
            cur = cur->_right;
        }
        else
        {
            return true;//在这中间，就说明找到了
        }
    }
    return false;//走到空就没找到
}

递归版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Node *FindR(const K &key)
{
    return _Find(_root, key);
}
Node *_FindR(Node *root, const K &key)
{
    if (root == nullptr)
    {
        return nullptr;
    }
    if (root->_val == key)
    {
        return root;
    }
    else if (root->_val > key)
    {
        return _FindR(root->_left, key);
    }
    else
    {
        return _FindR(root->_right, key);
    }
}

Erase

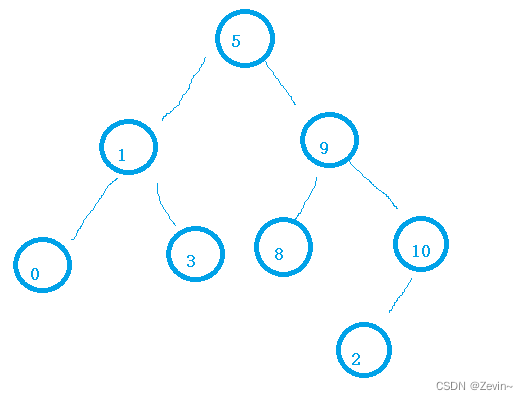
在这里插入图片描述

非递归版本

  1. 先找到要查找到要删除的节点
  2. 如果要删除的节点左子树为空，如果它是它父亲的左节点，它的父亲节点的左节点连接上删除节点的右指针

例如删除3，左为空，3是1的右节点，把1的右节点，连接到3的右节点

  1. 如果要删除的节点右子树为空，它为父节点的右节点，把它父节点的右节点连接到删除节点的左节点

例如删除10，右为空，10 是9的右节点，把10的左节点，连接到9的右节点上

  1. 如果要删除的节点左右子树都为空，要使用替换法删除，可以把要删除的节点的右子树的最左边或者要删除节点的左子树的最右边，把它和要删除节点进行替换，在把那个替换的节点删除

例如删除5，左右节点都不为空，把5右节点的最左边和5进行替换，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
bool Erase(const K &key)
{
    //先查找,删除之后要保持搜索二叉树的状态
    //有两个儿子，用左子树的最右节点，或者右子树的最左节点来进行替换删除
    //先找到要删除的值，还要找到它的父亲
    Node *cur = _root;
    Node *parent = nullptr;
    while (cur)
    {
        if (cur->_val < key)
        {
            parent = cur;
            cur = cur->_right;
        }
        else if (cur->_val > key)
        {
            parent = cur;
            cur = cur->_left;
        }
        else
        {
            //这里面就找到了
            //如果删除的是根节点，左为空，或右为空，没有父亲，我们还要单独处理

            if (cur->_left == nullptr) //左为空
            {
                if (parent == nullptr)//删除的是根节点
                {
                    _root = _root->_right;
                }
                else
                {
                    if (parent->_left == cur)
                    {
                        //我是父亲的左
                        //父亲的左，指向我的右
                        parent->_left = cur->_right;
                    }
                    else if (parent->_right == cur)
                    {
                        parent->_right = cur->_right;
                    }
                }
                delete cur;
                cur = nullptr;
            }
            else if (cur->_right == nullptr) //右为空
            {
                if (parent == nullptr)
                {
                    _root = _root->_left;
                }
                else
                {
                    if (parent->_left == cur)
                    {
                        //我是父亲的左
                        //父亲的左，指向我的右
                        parent->_left = cur->_left;
                    }
                    else if (parent->_right == cur)
                    {
                        parent->_right = cur->_left;
                    }
                }
                delete cur;
                cur = nullptr;
            }
            else
            {
                //都不为空
                //我们用右子树的最左节点,替换法删除
                Node *node = cur->_right;
                Node *parent = cur;
                if (node->_left != nullptr)//右子树右左节点
                {

                    while (node->_left)
                    {
                        parent = node;
                        node = node->_left;
                    }
                    swap(cur->_val, node->_val);
                    parent->_left = node->_right;
                    delete node;
                    node = nullptr;
                }
                else//右子树没有左节点，直接把父和它的右节点连接起来即可
                {
                    swap(cur->_val, node->_val);
                    parent->_right = node->_right;
                    delete node;
                    node = nullptr;
                }
            }

            return true;
        }
    }
    return false;
}

递归版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
Node *EraseR(const K &key)
{
    _EraseR(key, _root);
}
bool _EraseR(const K &key, Node *&root)
{
    if (root == nullptr)
        return false;
    if (root->_val > key)
    {
        return _EraseR(key, root->_left);
    }
    else if (root->_val < key)
    {
        return _EraseR(key, root->_right);
    }
    else
    {
        Node *del = root;
        if (root->_left == nullptr)
        {

            root = root->_right;
        }

        else if (root->_right == nullptr)
        {
            root = root->_left;
        }
        else
        {
            //左右都不为空
            //找到右子树的最左边，找替代节点

            Node *min = root->_right;
            while (min->_left)
            {
                min = min->_left;
            }
            swap(min->_val, root->_val); //把替代节点替换上去，后面只需要再递归的去删除交换的节点就可以了
            //递归到右子树的最左节点去删除
            return _EraseR(key, root->_right);
        }
        delete del;
        return true;
    }
}

InOrder

中序遍历，左根右
在类里面递归遍历，我们可以使用子函数，这样外部就不需要用类里面的私有成员变量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void InOrder()
{
    //套一个子函数就可以了
    _InOrder(_root);
}

void _InOrder(Node *root) //在外面或得不到根
{
    if (root == nullptr)
        return;
    _InOrder(root->_left);
    cout << root->_val << " ";
    _InOrder(root->_right);
}

KV模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
template <class K,class V>

struct BSTNode
{
    K _key;
    V _val;
    BSTNode<K,V> *_left;
    BSTNode<K,V> *_right;
    BSTNode(const K &key,const V& val)
        : _val(val), _right(nullptr), _left(nullptr),_key(key)
    {
    }
};

//比如：key是身份证，value就是票的信息，vector<info> _vinfo
template <class K,class V>
struct BSTree
{
    typedef BSTNode<K,V> Node;

private:
    Node *_root;

public:
    BSTree()
        : _root(nullptr)
    {
    }

    bool Insert(const K &key,const V& val) //非线性叫做insert
    {
        //插入重复的值，就返回失败
        if (_root == nullptr)
        {
            _root = new Node(key,val);
            return true;
        }
        else
        {
            Node *cur = _root;
            Node *prev;
            while (cur)
            {
                if (cur->_key > key)
                {
                    prev = cur;
                    cur = cur->_left;
                }
                else if (cur->_key < key)
                {
                    prev = cur;
                    cur = cur->_right;
                }
                else
                {
                    return false;
                }
            }
            cur = new Node(key,val);
            if (prev->_key < key)
            {
                prev->_right = cur;
            }
            else
            {
                prev->_left = cur;
            }
            return true;
        }
    }

    

    Node* Find(const K &key) //查找,返回对应的节点
    {
        Node *cur = _root;
        while (cur)
        {
            if (cur->_key > key)
            {
                cur = cur->_left;
            }
            else if (cur->_key < key)
            {
                cur = cur->_right;
            }
            else
            {
                return cur;//找到就返回对应的节点
            }
        }
        return nullptr;//没有找到就返回空
    }
    void InOrder()
    {
        //套一个子函数就可以了
        _InOrder(_root);
    }

    void _InOrder(Node *root) //在外面或得不到根
    {
        if (root == nullptr)
            return;
        _InOrder(root->_left);
        cout << root->_key << " ";
        _InOrder(root->_right);
    }

    bool Erase(const K &key)
    {
        //先查找,删除之后要保持搜索二叉树的状态
        //有两个儿子，用左子树的最右节点，或者右子树的最左节点来进行替换删除
        //先找到要删除的值，还要找到它的父亲
        Node *cur = _root;
        Node *parent = nullptr;
        while (cur)
        {
            if (cur->_key < key)
            {
                parent = cur;
                cur = cur->_right;
            }
            else if (cur->_key > key)
            {
                parent = cur;
                cur = cur->_left;
            }
            else
            {
                //这里面就找到了
                //如果删除的是根节点，左为空，或右为空，没有父亲，我们还要单独处理

                if (cur->_left == nullptr) //左为空
                {
                    if (parent == nullptr)
                    {
                        _root = _root->_right;
                    }
                    else
                    {
                        if (parent->_left == cur)
                        {
                            //我是父亲的左
                            //父亲的左，指向我的右
                            parent->_left = cur->_right;
                        }
                        else if (parent->_right == cur)
                        {
                            parent->_right = cur->_right;
                        }
                    }
                    delete cur;
                    cur = nullptr;
                }
                else if (cur->_right == nullptr) //右为空
                {
                    if (parent == nullptr)
                    {
                        _root = _root->_left;
                    }
                    else
                    {
                        if (parent->_left == cur)
                        {
                            //我是父亲的左
                            //父亲的左，指向我的右
                            parent->_left = cur->_left;
                        }
                        else if (parent->_right == cur)
                        {
                            parent->_right = cur->_left;
                        }
                    }
                    delete cur;
                    cur = nullptr;
                }
                else
                {
                    //都不为空
                    //我们用右子树的最左节点,替换法删除
                    Node *node = cur->_right;
                    Node *parent = cur;
                    if (node->_left != nullptr)
                    {

                        while (node->_left)
                        {
                            parent = node;
                            node = node->_left;
                        }
                        swap(cur->_val, node->_val);
                        swap(cur->_key, node->_key);
                        parent->_left = node->_right;
                        delete node;
                        node = nullptr;
                    }
                    else
                    {
                        swap(cur->_val, node->_val);
                        swap(cur->_key, node->_key);
                        parent->_right = node->_right;
                        delete node;
                        node = nullptr;
                    }
                }

                return true;
            }
        }
        return false;
    }

    
};
数据结构
#c++ 数据结构 算法
二叉搜索树
http://example.com/2022/08/28/二叉搜索树/
作者
Zevin
发布于
2022年8月28日
许可协议