跟着英雄学算法--矩阵

目录

1.力扣题分析

2.最富有客户的资产总量

3.转置矩阵 

4.旋转图像

5.回旋矩阵（方阵）

---

矩阵力扣题讲解

二进制二维数组image水平反转在取反

int** flipAndInvertImage(int** image, int imageSize, int* imageColSize, int* returnSize, int** returnColumnSizes){
    int i, j, col;
    int **ret = (int **)malloc( sizeof(int *) * imageSize );        // (1)
    *returnColumnSizes = (int *)malloc( sizeof(int) * imageSize );  // (2)
    for(i = 0; i < imageSize; ++i) {
        col = imageColSize[i];                                      // (3)
        ret[i] = (int *)malloc( sizeof(int) * col );                // (4)
        (*returnColumnSizes)[i] = col;                              // (5)
        for(j = 0; j < col; ++j) {
            ret[i][j] = 1 - image[i][ col-1-j ];                    // (6)
        }
    }
    *returnSize = imageSize;                                        // (7)
    return ret;                                                     // (8)
}

image是传过来二维数组，

imagesize是传过来的二维数组的行数，

imagecolsize是传过来二维数组每行的列数

returnSize是传回去二维数组的行数

returnColumnSizes是传回去二维数组每行的列数

返回的时候要malloc一个二维数组来接收

同时每行也要malloc处每行的元素个数（最后malloc完二维数组后，就对每个一维数组进行malloc）

1.最富有客户的资产总量

给你一个 m x n 的整数网格 accounts ，其中 accounts[i][j] 是第 i​​​​​​​​​​​​ 位客户在第 j 家银行托管的资产数量。返回最富有客户所拥有的 资产总量 。

客户的 资产总量 就是他们在各家银行托管的资产数量之和。最富有客户就是 资产总量 最大的客户。

示例 1：

输入：accounts = [[1,2,3],[3,2,1]]
输出：6
解释：
第 1 位客户的资产总量 = 1 + 2 + 3 = 6 第 2 位客户的资产总量 = 3 + 2 + 1 = 6 两位客户都是最富有的，资产总量都是 6 ，所以返回 6 。

示例 2：

输入：accounts = [[1,5],[7,3],[3,5]]
输出：10
解释：
第 1 位客户的资产总量 = 6
第 2 位客户的资产总量 = 10
第 3 位客户的资产总量 = 8
第 2 位客户是最富有的，资产总量是 10

示例 3：

输入：accounts = [[2,8,7],[7,1,3],[1,9,5]]
输出：17

思路：求出每行的和，再将每行和进行比较，求出最大值进行返回

int maximumWealth(int** accounts, int accountsSize, int* accountsColSize){
int i,j,col;
int arr[accountsSize];//用一个arr数组来接收每行和
memset(arr,0,accountsSize*sizeof(int));同时要对他初始化为0

int max;//定义max为最终最大返回值
for(i=0;i<accountsSize;i++)
{
    
    for(j=0;j<accountsColSize[i];j++)
    {
        arr[i]+=accounts[i][j];
    } 
}
max=arr[0];//max赋初值第一个元素
for(i=0;i<accountsSize;i++)
{
    if(max<arr[i])
    {
        max=arr[i];
    }
}
return max;

}

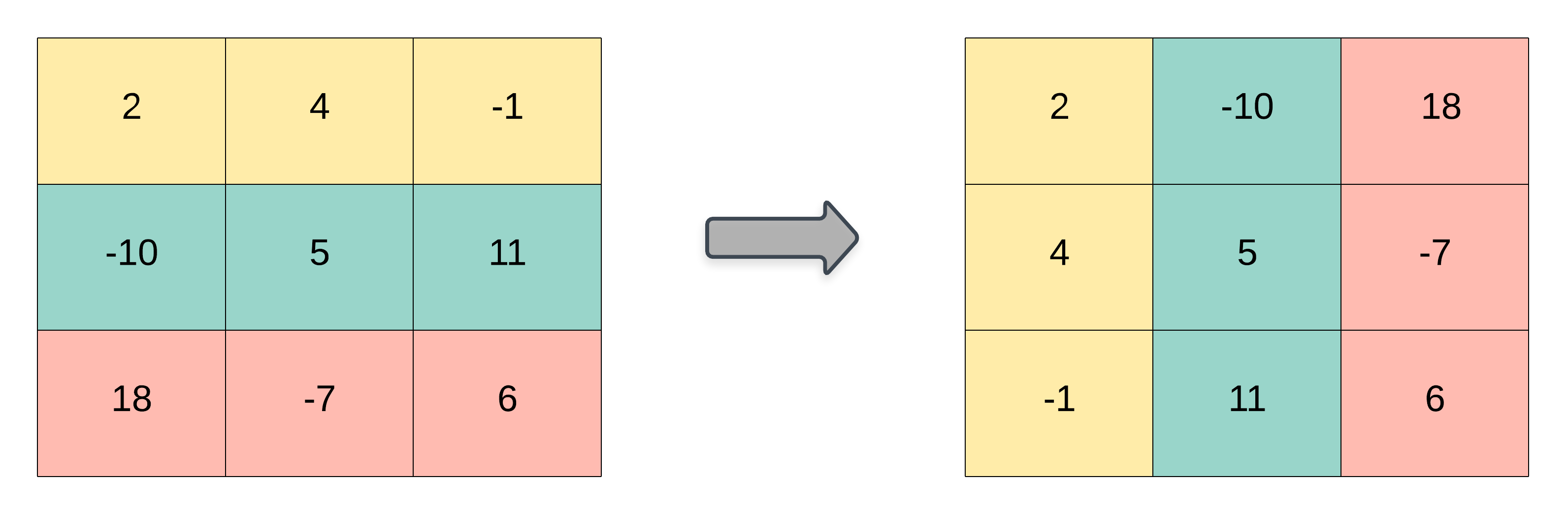
转置矩阵

给你一个二维整数数组 matrix， 返回 matrix 的 转置矩阵 。

矩阵的 转置 是指将矩阵的主对角线翻转，交换矩阵的行索引与列索引。

示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[1,4,7],[2,5,8],[3,6,9]]

示例 2：

输入：matrix = [[1,2,3],[4,5,6]]
输出：[[1,4],[2,5],[3,6]]

 思路：对角线互换，行变列，列变行

 1.returnsize返回的是转置后返回的二维数组的行数；

2.*returnColumnSizes是返回的二维数组的每行的列数

3.返回的二维数组必须自己malloc出来，同时返回的二维数组每一行的元素也要自己malloc出来，

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
int** transpose(int** matrix, int matrixSize, int* matrixColSize, int* returnSize, int** returnColumnSizes)
{
int i,j,col;    
col=matrixColSize[0];//
int **ret=(int **)malloc(sizeof(int*)*col);      //ret的行数是matrix的列数
*returnColumnSizes=(int*)malloc(sizeof(int)*col);//*returnColumnSize返回的每行的个数是原二维数组的列数
*returnSize=col;      //返回的行数是原来的列数                        
for(i=0;i<col;i++)      
{          
    (*returnColumnSizes)[i]=matrixSize;//返回每行的列数是原来的行数
    ret[i]=(int *)malloc(sizeof(int)*matrixSize);
}
for(i=0;i<matrixSize;i++)
{    
    for(j=0;j<col;j++)
    {
        ret[j][i]=matrix[i][j];
    }
}
return ret;
}

旋转图像

给定一个 _n _× n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在** 原地** 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

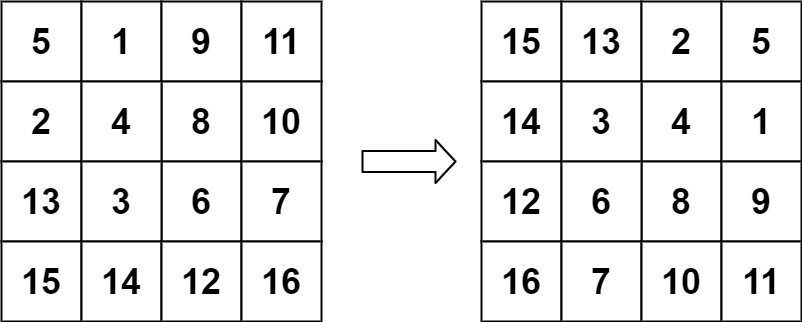
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

示例 3：

输入：matrix = [[1]]
输出：[[1]]

示例 4：

输入：matrix = [[1,2],[3,4]]
输出：[[3,1],[4,2]]

void rotate(int** matrix, int matrixSize, int* matrixColSize){
int i=0;
int j=0;
int col;
int arr[matrixSize][matrixSize];//开辟一个arr二维数组，长度是matrixsize
for(i=0;i<matrixSize;i++)
{
    col=matrixColSize[i];       //col是每行的列数
for(j=0;j<col;j++)
{
    arr[j][col-1-i]=matrix[i][j];//因为是对matrix的i和j的遍历，所以matrix是[i][j],
                                   arr是规律是arr[j][col-1-i]
}
}
for(i=0;i<matrixSize;i++)
{
    col=matrixColSize[i];
    for(j=0;j<col;j++)
    {
        matrix[i][j]=arr[i][j];//arr是已经旋转之后的数组，同时因为要旋转，所以要对原来的数组进行改变，把arr赋给matrix
    }
}
return matrix;
}

回旋矩阵

int main()
{
	int i, j;
	int m = 3;
	int n = 3;

	int ret[10][10];
	memset(ret, 0, sizeof(ret));用memset内存函数对ret初始化为0
	

	int count = 1;
	for (i = 0; i < n / 2; i++)
	{
		
		//向右
		for (j = i; j < m - i; j++)
		{
			ret[i][j] = count++;
		}
		//向下
		for (j = i + 1; j < n - i; j++)
		{
			ret[j][m - 1 - i] = count++;
		}
		for (j = m - 2 - i; j >= i; j--)
		{
			ret[n - 1 - i][j] = count++;
		}
		for (j = n - 2 - i; j > i; j--)

		{

			ret[j][i] = count++;
		}
		if (n % 2 == 1)//假如n是奇数的话，中间还要填一个数
		{
			ret[n / 2][m / 2] = n * m;
		}

	}
	
	for (i = 0; i < n; i++)
	{
		for (j = 0; j < m; j++)
		{
			printf("%d ", ret[i][j]);
		}
		printf("\n");
	}